티스토리 뷰
Set
특징
Set은 중복을 허용하지 않음(중복제거, unique한 값을 가짐)Set은 순서가 없음
Set 만들기
>>> s1 = set() # 빈 set 만듬
>>> s1
set()
>>> s2 = set([1, 2, 1, 3])
>>> s2
{1, 2, 3}
# 또는
>>> s2 = set(range(1, 4))
>>> s3 = {1, 2, 1, 3}
>>> s3
{1, 2, 3}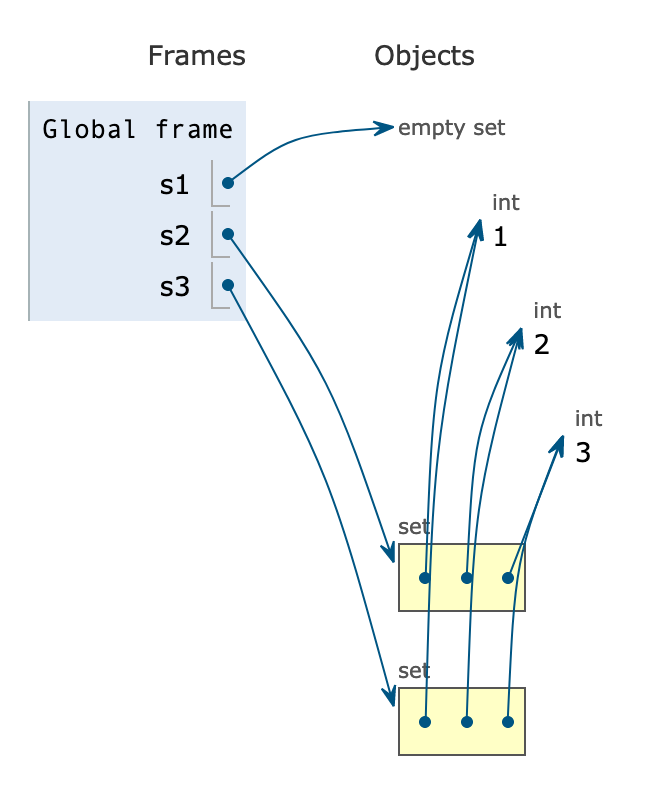
아이템 추가
>>> s = set()
>>> s.add(1)
>>> s.add(2)
>>> s.add(1)
>>> s
{1, 2}여러 아이템 추가 한번에 추가
>>> s = set()
>>> s.update([1, 2, 3])
>>> s
{1, 2, 3}아이템 가져오기
.pop()을 사용하면 맨 왼쪽의 아이템이 반환되고 지워짐set은 순서가 없기 때문에 index를 사용하여 아이템을 가져 올 수 없음
>>> s = {1, 2, 3, 4}
>>> s.pop()
1
>>> s
{2, 3, 4}아이템 제거
.remove() 사용
>>> s = set([1, 2, 3])
>>> s.remove(1)
>>> s
{2, 3}
>>> s.remove(1) # key error 발생
KeyError: 1.discard() 사용
>>> s = {1, 2, 3}
>>> s.discard(1)
>>> s
{2, 3}
>>> s.discard(1) # 아이템이 없어도 에러 발생 안함.clear() 사용
전체 아이템을 삭제
>>> s = {1, 2, 3}
>>> s.clear()
>>> s
set()연산
>>> s1 = set([1, 2, 3, 4, 5, 6])
>>> s2 = set([4, 5, 6, 7, 8, 9])교집합
>>> s1 & s2
{4, 5, 6}
>>> s1.intersection(s2)
{4, 5, 6}
>>> s2.intersection(s1)
{4, 5, 6}
>>> s1 &= s2 # 교집한 후 s1에 대입
>>> s1
{4, 5, 6}합집합
>>> s1 | s2
{1, 2, 3, 4, 5, 6, 7, 8, 9}
>>> s1.union(s2)
{1, 2, 3, 4, 5, 6, 7, 8, 9}
>>> s2.union(s1)
{1, 2, 3, 4, 5, 6, 7, 8, 9}
>>> s1 |= s2 # 합집합 후 s1에 대입
>>> s1
{1, 2, 3, 4, 5, 6, 7, 8, 9}차집합
>>> s1 - s2
{1, 2, 3}
>>> s2 - s1
{8, 9, 7}
>>> s1.difference(s2)
{1, 2, 3}
>>> s2.difference(s1)
{8, 9, 7}
>>> s1 -= s2 # 차집합 후 s1에 대입
>>> s1
{1, 2, 3}대칭차집함
합집합과 교집합을 따로 실행 후 합집합에서 교집합 빼기(합집합 - 교집합)
>>> s1 ^ s2
{1, 2, 3, 7, 8, 9}
>>> s1.symmetric_difference(s2)
{1, 2, 3, 7, 8, 9}
>>> s2.symmetric_difference(s1)
{1, 2, 3, 7, 8, 9}
>>> s1 ^= s2 # 대칭차집합 후 s1에 대입
>>> s1
{1, 2, 3, 7, 8, 9}Set 메서드
.issubset()
부분 집합 여부 확인
>>> s1 = {1, 2, 3, 4, 5}
>>> s2 = {1, 2, 3}
>>> s1.issubset(s2)
False
>>> s2.issubset(s1)
True.issuperset()
.issubset()의 반대(포함 여부 판단)
>>> s1 = {1, 2, 3, 4, 5}
>>> s2 = {1, 2, 3}
>>> s1.issuperset(s2)
True
>>> s2.issuperset(s1)
False.isdisjoint()
교집합이 없으면 True, 있으면 False
>>> s1 = {1, 2, 3, 4, 5}
>>> s2 = {1, 2, 3}
>>> s1.isdisjoint(s2)
True
>>> s2.isdisjoint(s1)
True
>>> s1 = {1, 2, 3}
>>> s2 = {4, 5, 6}
>>> s1.isdisjoint(s2)
False
>>> s2.isdisjoint(s1)
FalseSet 복사
>>> s = {1, 2, 3}
>>> c = s.copy()
>>> s
{1, 2, 3}
>>> c
{1, 2, 3}
>>> id(s)
4554012032
>>> id{c}
4554012704
>>> s = set(1, 2, 3)
>>> c = set(s)
>>> s
{1, 2, 3}
>>> c
{1, 2, 3}
>>> id(s)
4554012032
>>> id(c)
4554012928Comprehensions
>>> l = [1, 2, 3, 4, 5]
>>> {i for i in l}
{1, 2, 3, 4, 5}frozenset
한번 만들어 지면 변경할 수 없는 set(immutable)
아이템을 추가하거나 변경하는 메서드를 제공하지 않음(add, remove, pop, clear, update)
>>> s = frozenset() # 빈 set
>>> s = frozenset([1, 2, 3])
>>> s = frozenset(range(1, 4))연산
set의 연산법과 같음
>>> s1 = frozenset([1, 2, 3, 4, 5])
>>> s2 = frozenset([4, 5, 6, 7, 8])
# 교집합
>>> s1 & s2
frozenset({4, 5})
>>> s1.intersection(s2)
# 합집합
>>> s1 | s2
frozenset({1, 2, 3, 4, 5, 6, 7, 8})
>>> s1.union(s2)
frozenset({1, 2, 3, 4, 5, 6, 7, 8})
# 차집합
>>> s1 - s2
frozenset({1, 2, 3})
>>> s1.difference(s2)
frozenset({1, 2, 3})
# 대칭차집합
>>> s1 ^ s2
frozenset({1, 2, 3, 6, 7, 8})
>>> s1.symmetric_difference(s2)
frozenset({1, 2, 3, 6, 7, 8})메서드
.issubset()
부분 집합 여부 확인
>>> s1 = frozenset([1, 2, 3, 4, 5])
>>> s2 = frozenset([1, 2, 3])
>>> s1.issubset(s2)
False
>>> s2.issubset(s1)
True.issuperset()
.issubset()의 반대(포함 여부 판단)
>>> s1 = frozenset([1, 2, 3, 4, 5])
>>> s2 = frozenset([1, 2, 3])
>>> s1.issuperset(s2)
True
>>> s2.issuperset(s1)
False.isdisjoint()
교집합이 없으면 True, 있으면 False
>>> s1 = frozenset([1, 2, 3, 4, 5])
>>> s2 = frozenset([1, 2, 3])
>>> s1.isdisjoint(s2)
True
>>> s2.isdisjoint(s1)
True
>>> s1 = frozenset([1, 2, 3])
>>> s2 = frozenset([4, 5, 6])
>>> s1.isdisjoint(s2)
False
>>> s2.isdisjoint(s1)
False복사
>>> s = frozenset([1, 2, 3])
>>> c = s.copy()
>>> s
frozenset({1, 2, 3})
>>> c
frozenset({1, 2, 3})
>>> id(s)
4581973344
>>> id(c)
4581973344'Basic' 카테고리의 다른 글
| 파이썬 조건문 그리고 반복문 (0) | 2020.04.26 |
|---|---|
| 파이썬 Tuple (0) | 2020.04.19 |
| 파이썬 Dictionary (0) | 2020.04.19 |
| 파이썬 List (0) | 2020.04.12 |
| 파이썬 String (0) | 2020.04.11 |
최근에 올라온 글
글 보관함
